
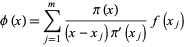
is the ith Hermite polynomial, and is the corresponding discrete set (or abscissas) which evaluates the integral exactly for Here, and are the dimensionless variables of microscopic velocity v and macroscopic velocity u, respectively, in which R is the gas constant and T is the temperature. According to the Hermite polynomial expansion, for nth-moment-order ED discretization which restores u n moment integral, its can be expressed as The ED discretization has been investigated in-depth and a lot of excellent theories have been proposed, such as the small-Mach-number approximation, the Hermite polynomial expansion, and the entropic LB model. This enables us to focus on the unidimensional Cartesian model to simplify our framework. Under a Cartesian coordinate system, multidimensional can always be constructed as a tensor product of the unidimensional. In practice, this velocity discretization can be achieved by constructing a set of equilibrium distributions on a discrete velocity set i.e., equilibrium distribution (ED) discretization. With specific discretization of the continuous BGK–Boltzmann equation in velocity space (i.e., on-node lattices), each collision-streaming proceeding would locate on nodes, achieving a simple but efficient “stream along links and collide at nodes” algorithm, while the corresponding macroscopic dynamics such as the Navier–Stokes equations can be properly recovered. Equation ( 1) can be treated as a characteristic integral of the Bhatnagar–Gross–Krook (BGK)–Boltzmann equation along, depicting the microscopic dynamic of particles. Where and are, respectively, the population and equilibrium distribution corresponding to the discrete velocity. The essence of the LB method is an intuitively parallel collision-streaming algorithm with discretized position, time t, and microscopic velocity The lattice Boltzmann (LB) method is a powerful approach for hydrodynamics. It is also worth noting that pGHQ can be extended into the entropic LB model, even though it was proposed for the Hermite polynomial expansion LB theory. Hence, the results of the pGHQ scheme lay a foundation for further investigations to improve the numerical stability of the LB method by modifying the discrete velocity set. Through a brief analysis, the discrete velocity set shows a significant influence on the positivity of equilibrium distributions, which is considered as one of the major impacts of the numerical stability of the LB method. The search reveals a surprising abundance of available lattices. We employ the pGHQ scheme to search the local optimal and asymmetric lattices for moment degree equilibrium distribution discretization on the range. Compared with the existing approaches, the pGHQ scheme has the following advantages: extremely concise algorithm, unifies the constructing procedure for symmetric and asymmetric on-node lattices, and covers a full-range quadrature degree of a given discrete velocity set. A concise theoretical framework, the partial Gauss–Hermite quadrature (pGHQ), is established to construct on-node lattices of the lattice Boltzmann (LB) method under a Cartesian coordinate system.


 0 kommentar(er)
0 kommentar(er)
